Deep neural network

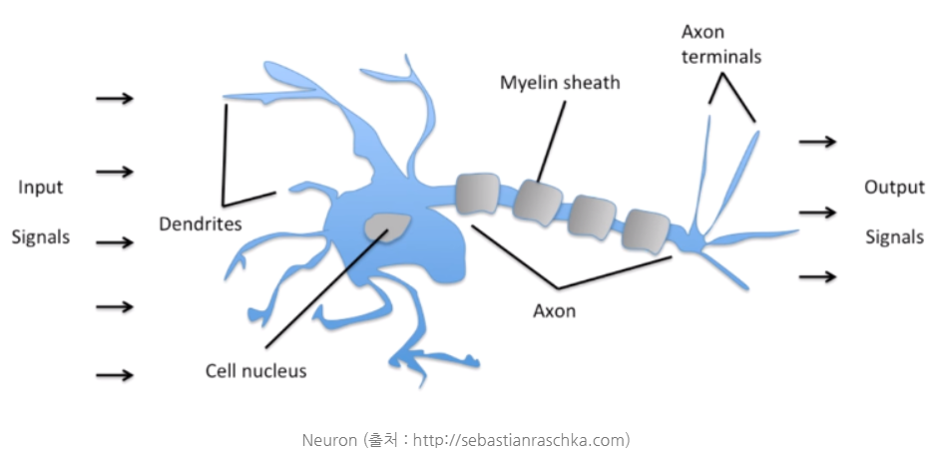
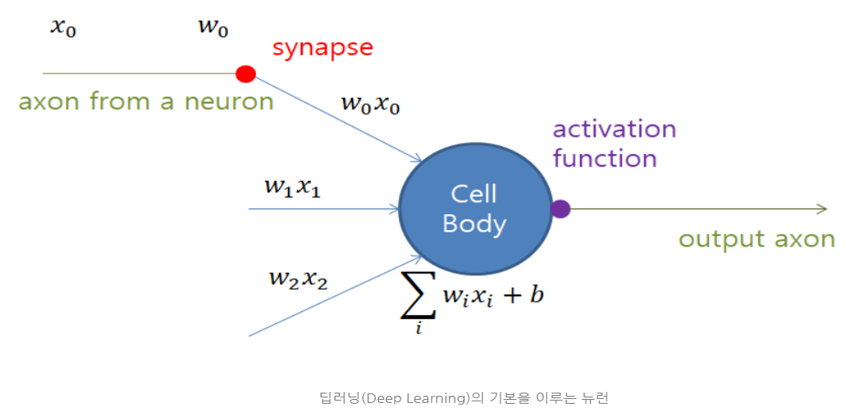
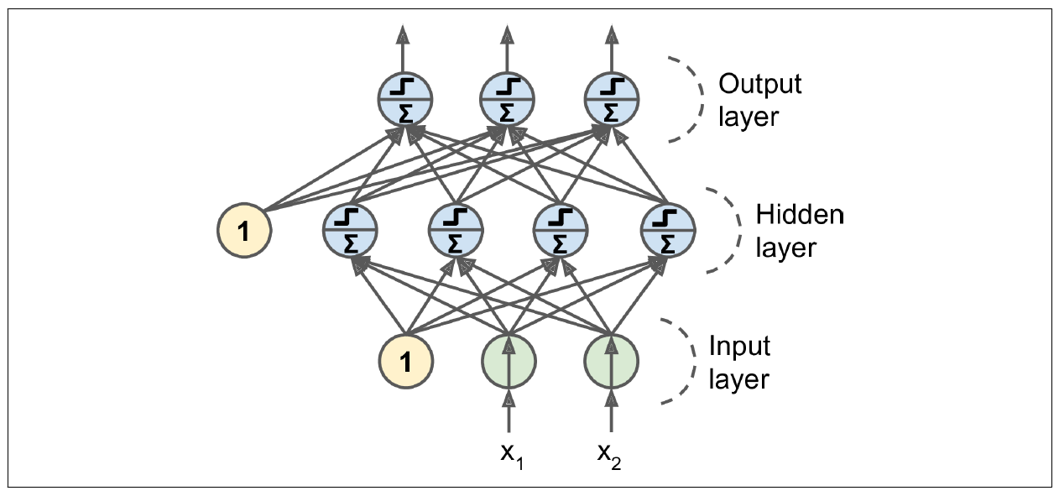
• ANN에서 Input layer와 Output layer를 제외한 중간 layer들을 모두 hidden layer라고 하며, hidden layer의 개수가 2개 이상이면 DNN이라 한다.
• Output layer를 제외하고는 모두 bias 뉴런을 포함하며 다음 층과 연결 되어있다.

손실 함수(loss or cost function)

• 네트워크(모델) 구조가 정해지면 모델이 학습을 진행하기 위해서는 손실 함수를 정의 해야 한다.
• 손실함수는 네트워크의 출력과 우리가 원하는 값의 차이를 의미하며, 주로 아래 두 함수들로 정의된다.
• 손실함수의 종류
  • 평균 제곱 오차(Mean Squared Error, MSE) : 주로 회귀(regression)에 사용
  $$ Error\quad =\quad \frac { 1 }{ n } \sum _{ k }^{ n }{ { ({ y }_{ k }-{ t }_{ k }) }^{ 2 } } $$
  • 교차 엔트로피 오차(Cross Entropy Error, CEE) : 주로 분류(classification)에 사용
  $$ Error\quad =\quad \frac { 1 }{ n } \sum _{ k }^{ n }{ { { t }_{ k } }\log { { y }_{ k } } } $$

경사 하강법(Gradient Descent)

• 손실 함수를 최소로 하는 매개변수를 찾기 위한 알고리즘으로 경사 하강법(이하 GD)을 사용한다.
• Neural Network에서 매개변수는 각 layer의 weight와 biase이다.
• 알고리즘
  1. 매겨변수를 초기화한다.
  2. 손실 함수를 미분하여 기울기를 계산한다.
  3. 기울기에 learning rate를 곱하여 매개변수를 변경한다. $$ { W }_{ n }:={ W }_{ n-1 }-\alpha \frac { \partial }{ \partial W } cost(W) $$
  4. 위 과정을 허용오차(tolerance)까지 반복한다.
  
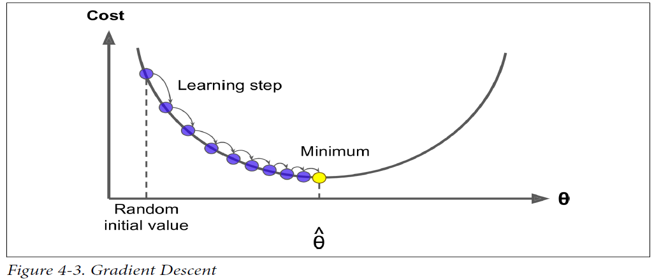
• GD는 일반적으로 많이 사용되며 Batch GD, Stochastic GD 등의 응용이 있다.
• 주의
  • 정의된 손실 함수는 미분 가능 해야 한다.
  • gradient가 너무 작으면 학습 속도가 느려진다.
  • 반대로 gradient가 너무 커지면 발산하여 학습이 정상적으로 이루어지지 않는다.
  • 이를 위해 learning rate 설정하고 학습을 진행해야 한다.
  
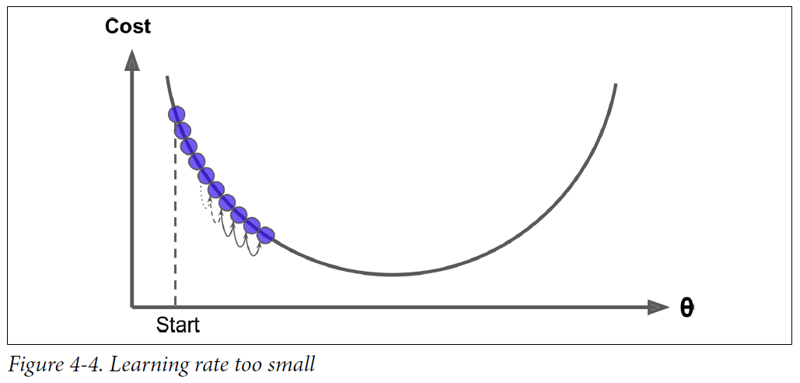
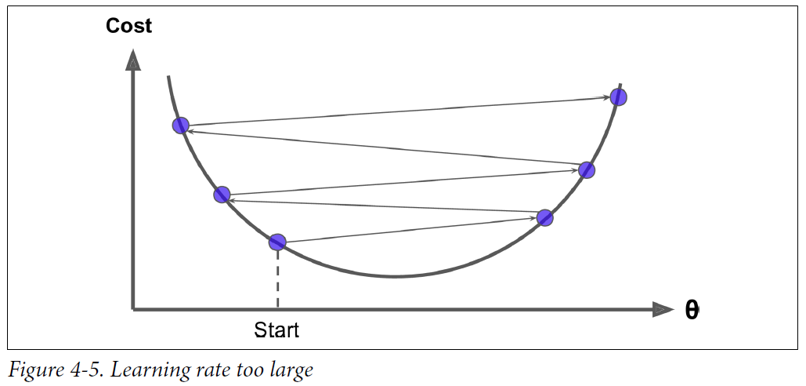
• 즉, 머신러닝에서 학습이란 손실함수를 최소화하는 모델 파라미터를 찾는 과정 이라고 할 수있다.

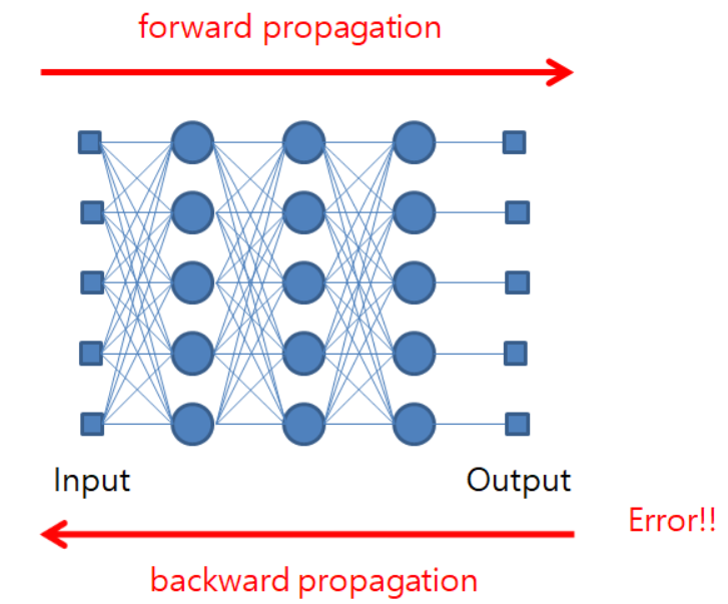
역전파(Back-propagation)

• 앞서 보다시피 딥러닝은 다양한 네크워트 구조를 가질 수 있다.
• 그렇다면, GD으로 구한 gradient를 각 weight와 bias에 어떻게 적용 해야할까?
• Back-propagation은 Neural Network에서의 gradient decent를 적용하기 위해 gradient를 계산하는 알고리즘이다.
• 알고리즘
  • 매개변수를 초기화한다.
  • 입력 데이터를 매개변수와 계산하여 각 층의 뉴런마다 출력을 얻는다. (forward propagation)
  • 출력 데이터와 정답 사이의 오차를 계산한다.
  • 역방향으로 각 layer을 거치면서 각 연결(매개변수)이 오차에 기여한 정도(gradient)를 측정한다. (back-propagation)
  • 오차가 감소하도록 매개변수를 조금씩 조정한다. (gradient decent)
  • 위 과정을 허용오차(tolerance)까지 반복한다.
  
• 한 노드에 대한 back-propagation
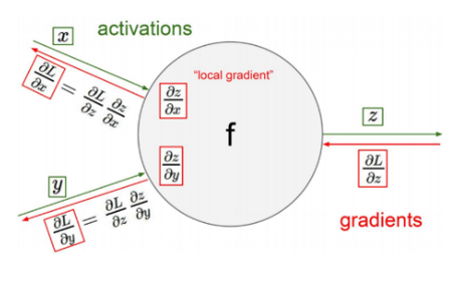
  • \(x,y\) : 해당 노드의 input
  • \(f\) : 해당 노드의 연산자
  • \(z\) : 해당 노드의 output
  • \(L\) : 계산되어진 손실 값
• 예를 들어, 3 layer DNN이 있다고 하자. 구조는 다음과 같다.
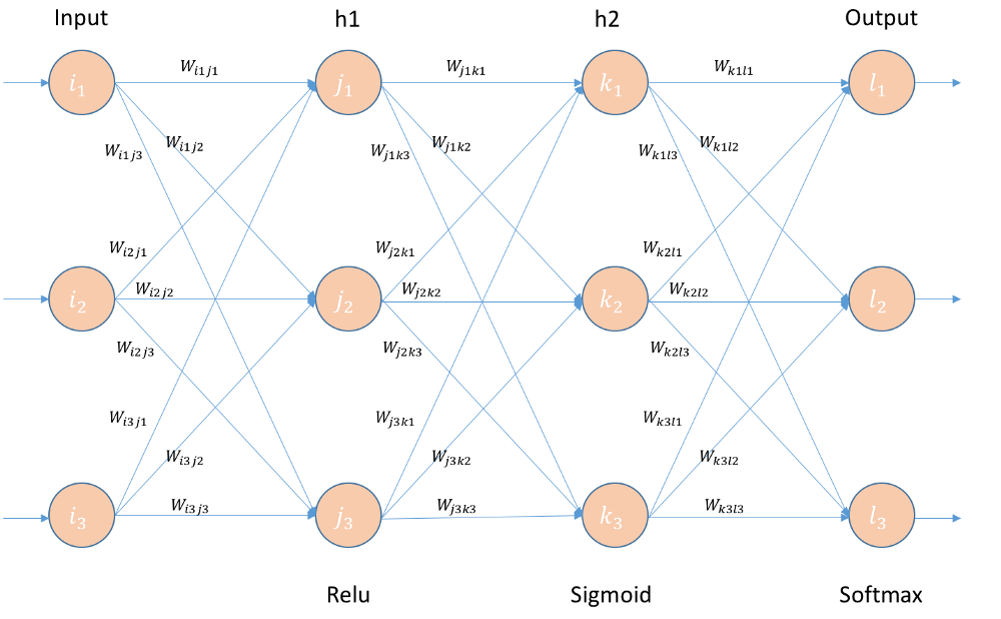
• 다음 그림은 hidden layer2와 output layer 사이의 back-propagation을 보여준다.
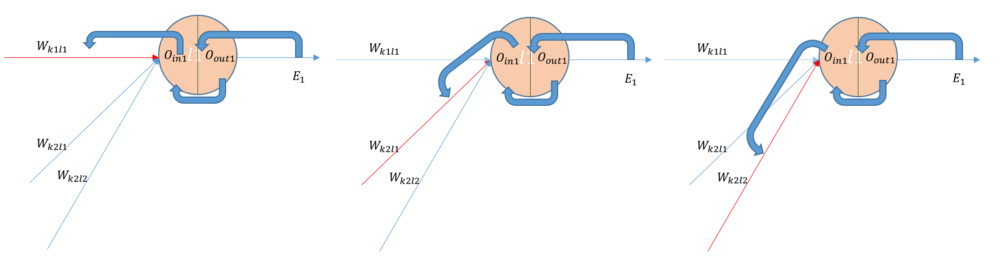
  • forward-propagation을 통해 계산된 \(loss({E}_{1})\)를 미분하여 해당 그레디언트를 각각 connection의 weight로 넘겨준다.
  
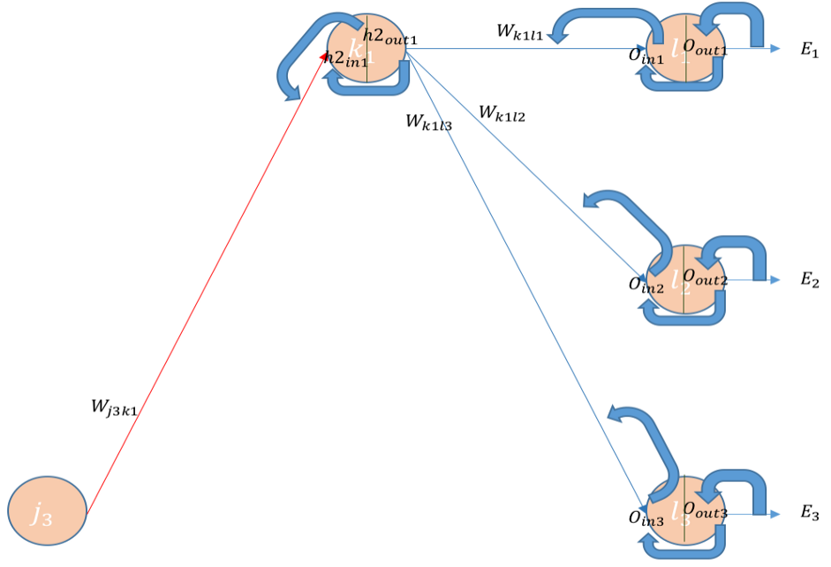
  • 전달된 그레디언트를 그 다음 layer로 넘겨주며 해당 전파는 input layer까지 진행된다.
  • gradient가 input layer까지 전달된 후 gradient descent를 적용하여 매개변수를 변경한다.
• 앞선 과정에서 각 layer별로 gradient를 계산해야 하기 때문에 활성함수는 미분 가능 해야한다.
• 계단 함수는 사용할 수 없으며, 대신 시그모이드 함수를 사용 할 수 있다.
• 그 외에도 다양한 활성 함수들을 사용할 수 있다.

여기까지만 해서 학습이 잘 되면 얼마나 좋을까…

우리 딥러닝 학습의 여정은 순탄치 않았는데…

[다음 편 예고] gradient가 자꾸 지멋대로 집을 나가거나 열폭해요

참고 자료

• http://it.plusblog.co.kr/221243889886
• https://mattmazur.com/2015/03/17/a-step-by-step-backpropagation-example/
• https://medium.com/@14prakash/back-propagation-is-very-simple-who-made-it-complicated-97b794c97e5c

본 포스팅은 머신러닝을 공부하면서 모델에 대한 개인적인 내용을 정리한 것이기 때문에 일반적인 용어 및 개념과 상이 할 수 있습니다.

모델링의 정의

• 어떤 물리현상을 특정한 목적에 맞추어 이용하기 쉬운 형식으로 표현하는 일 (두산백과)

위 정의를 실제 머신러닝 사례에 적용해 이해 해보자.
얼굴 이미지를 통해 사람을 인식하는 시스템을 만든다고 하자.
위 정의에 따라 현상과 목적, 형식에 대해 생각해보자.

여기서 주어진 현상이란 얼굴 이미지이며, 특정한 목적이란 사람을 정확하게 인식하는 것이다. 그렇다면 형식이란 무엇일까? 우리는 이것을 모델이라고 흔히 부른다. 또한, 대부분 모델은 하나의 목적 함수로써 표현되어 진다.

정리하면 아래와 같다.

• 현상이란 기록 되어진 데이터이다.
• 머신러닝 모델이란 데이터를 기반으로 특정 목적에 맞춰 원하는 결과를 줄 것이라고 기대하는 함수이다.
• 모델링이란 이와 같은 모델을 찾아가는 과정이다.

Neural Network의 정의

• 인간의 뇌를 구성하는 기본 단위인 뉴런(neuron)을 모방한 네트워크

뉴런의 구조

• 수상 돌기(Dendrites)에서 외부 신호를 수용하고 축색 돌기(Axon)을 통해 신호를 출력한다.

뉴런 구조 모델링

• 뉴런에 있는 각 축색돌기들은 시냅스(synapse)라고 하는 접점을 통해 외부 뉴런과 연결된다.
• 뉴런은 입력으로 들어오는 여러 개의 신호들을 하나로 합산한 다음 활성함수(Activation Function)을 통해 다시 다른 뉴런의 입력으로 들어가게 된다.
• 위와 같은 뉴런을 여러 개로 구성하여 네트워크를 구성할 수 있으며 ANN(Artificial Neural Network)이라 한다.

퍼셉트론

• ANN의 가장 기본 구조 중 하나로 입력에 각각 가중치를 곱하고 합치고 계단함수(활성함수)를 적용하여 그 결과(y)를 출력합니다.
• \[\quad y\quad =\quad \left\{ \begin{matrix} 0,\quad ({ w }_{ 1 }{ x }_{ 1 }\quad +\quad { w }_{ 2 }{ x }_{ 2 })\quad <\quad \theta \\ 1,\quad ({ w }_{ 1 }{ x }_{ 1 }\quad +\quad { w }_{ 2 }{ x }_{ 2 })\quad \ge \quad \theta \end{matrix} \right (단, \theta 는 계단함수의 임계치)\]

퍼셉트론으로 논리회로 학습

• AND 게이트의 진리표

• 위 진리표를 만족하는 모델(퍼셉트론)의 매개 변수인 (𝑤_1,𝑤_2, 𝜃)의 조합은 (0.5, 0.5, 0.7), (0.5, 0.5, 0.8), (1.0, 1.0, 1.0)등 무수히 많다.
• NAND 게이트와 OR 게이트 또한 특정 매개 변수가 주어지면 표현 가능하다.
• XOR 게이트는 표현 불가능하다. (단일 퍼셉트론은 비선형 영역을 표현할 수 없다.)
• 실제 데이터 분석(머신러닝) 과정 중에서는 학습 단계에서 적절한 매개 변수를 찾아간다.

참조 : 밑바닥부터 시작하는 딥러닝 - 사이토 코키

본 포스팅은 python 3.8 변경사항 중 assignment expressions와 positional-only parameters의 내용을 정리 했습니다.

assignment expressions

assigment expressions을 사용하면 if문, while문의 조건부에서 변수를 직접 할당하여 사용할 수 있다.

• assigment expressions 미사용

n = len(a)
if n > 10:
    print(f"List is too long ( %d elements, expected <= 10)" % n)

• assigment expressions 사용

if (n := len(a)) > 10:
    print(f"List is too long ({n} elements, expected <= 10)")
    

• if문 안에서만 사용될 변수라면 위와 같이 assigment expressions으로 짧게 코딩 할 수 있다.

positional-only parameters

positional-only parameters를 사용하면 함수 정의시 파라미터 더욱 명시적으로 작성 할 수 있다.
파라미터 정의 부분에 / 추가하게 되면 / 이전 파라미터는 키워드 명시 없이 순서대로 들어가야 하며, 다음 지정된 파리미터에 대해서는 키워드 명시를 강제한다.

• positional-only parameters 예시

def f(a, b, /, c, d, *, e, f):
    print(a, b, c, d, e, f)

• 가능한 함수 호출 예시

f(10, 20, 30, d=40, e=50, f=60)

• 불가능한 함수 호출 예시

f(10, b=20, c=30, d=40, e=50, f=60)   # b 키워드 할당 하면 안됨
f(10, 20, 30, 40, 50, f=60)           # e 키워드에 할당 해야함

• positional-only parameters의 장점
  • 키워드를 명시해야하는 파라미터와 아닌 파라미터를 구분하여 함수를 정의 할 수 있다.
  • readablity를 위해 키워드 명시가 불필요한 파라미터에 대해 명시를 하지 않도록 강제할 수 있다.
  • 함수 호출시 파라미터 입력에 대한 validation을 강화 할 수 있다.(변수를 잘못된 순서로 할당 한다든지…)

그 외 변경 사항

• Parallel filesystem cache for compiled bytecode files
• f-strings support = for self-documenting expressions and debugging
• PEP 578: Python Runtime Audit Hooks
• PEP 587: Python Initialization Configuration
• Vectorcall: a fast calling protocol for CPython
• Pickle protocol 5 with out-of-band data buffers¶
• etc..

참조 : https://docs.python.org/ko/3.8/whatsnew/3.8.html