Study for Data Science

Deep Neural Network(3)

13 Nov 2019 | neural network loss function gradient decent gradient vanishing/exploding

DNN의 문제점

최근의 DNN은 상당히 좋은 성능을 보이지만 초창기에는 몇몇 문제점이 있었다.
DNN 구조를 구성할 때 layer를 많이 쌓으면서 다음과 같다.

  • Vanishing gradient
  • Exploding gradient
  • 학습 속도가 느리다.
  • 많은 매개변수를 가지게 되면서 Overfitting을 하게 된다.

이런 문제점을 해결하기 위해 다음과 같은 다양한 방법에 대해 소개하려고 한다.

  • 가중치 초기화
  • 활성 함수 변경
  • 배치 정규화
  • 최적화 알고리즘 변경

Vanishing & Exploding Gradient problem

  • DNN의 학습 단계에서 경사 하강법으로 back-propagation을 통해 하위층으로 진행될 때, 아래와 같은 문제로 학습이 제대로 되지않는다.
    • 그레디언트가 점점 작아지면 가중치가 변경되지 않아 학습이 진행되지 않는 경우가 많이 발생한다.(Vanishing Gradient)
    • 반대로 그레디언트가 점점 커져 여러 개의 층이 비정상적으로 큰 가중치로 갱신되어 발산하게 된다.(Exploding Gradient)
  • 세이비어 글로럿과 요슈아 벤지오의 논문 “Understanding the Difficulty of Training Deep Feedforward Neural Networks”(2010)에서 다음과 같은 문제점을 제시한다.

문제 원인

  • 각 layer를 통과하면서 입력값의 분산보다 출력값이 분산이 커짐
  • 활성 함수로 시그모이드 함수를 사용하면서 입력의 분산이 커질 수록 0,1에 가까워 짐
  • 평균이 0.5라는 점과 함수가 항상 양수를 출력하기 때문에 문제 발생(편향 이동)

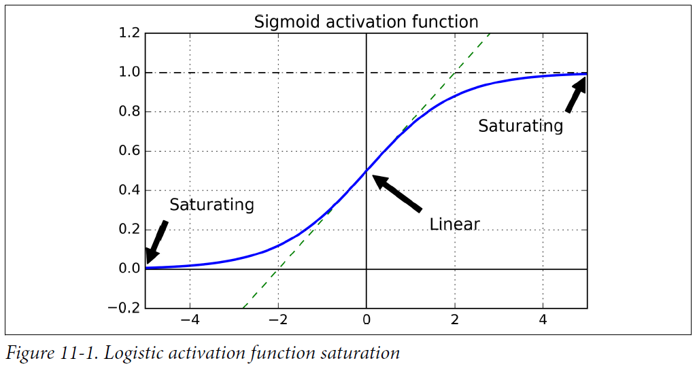
해결 방안

  • 가중치 초기화 방법 변경
    • 세이비어 초기화
      • 평균이 0이고 표준편차가 \(\sigma = \sqrt { \frac { 2 }{ { n }_{ input }+{ n }_{ output } } }\) 인 정규분포에서 무작위로 초기화
    • he 초기와
    • 그 외 활성 함수에 따라 다양한 초기화 방법이 있다.
  • 활성 함수 변경
    • 하이퍼볼릭 탄젠트 : \(\tanh { (x)\quad =\quad \frac { 2 }{ 1+{ e }^{ -2x } } -1 }\)
      • 장점 : 편향 이동이 발생하지 않는다.
      • 단점 : 시그모이드와 마찬가지로 𝑥 의 절대값이 커지면 그레디언트가 0에 수렴.
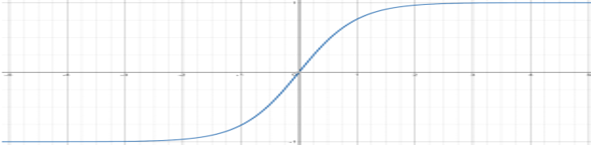
    • ReLU(rectified linear units) : \(ReLU(x)\quad =\quad max(0,x)\)
      • 장점 : 계산이 간단하며 그레디언트가 유지된다.
      • 단점 : 𝑥 <0일 때, 그레디언트가 0이 되어 가중치를 변화하지 못하고 0만 출력하게 된다. (dying \(ReLU\))
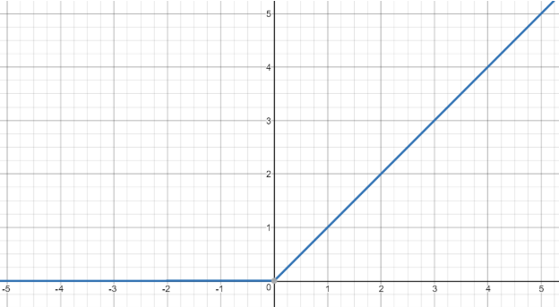
    • LeakyReLU : \(LeakyReLU(𝑥)=max(0.01x,x)\)
      • 장점 : dying \(ReLU\) 해결(\(x < 0\) 일 때, 그레디언트가 0이 아님.)
      • 단점 : 0에서 미분 불가
      • 참고) 기타 \(LeakyReLU $4의 변종도 있음,\) RReLU \((randomized leaky ReLU)/\) PReLU $$(parametric leaky ReLU)
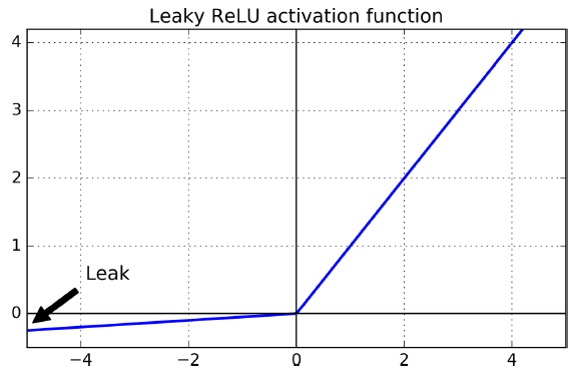
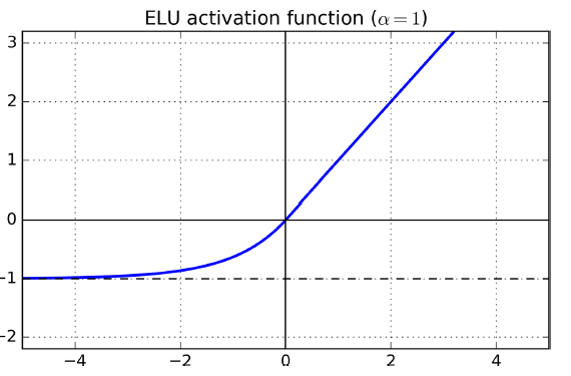
    • ELU : \({ ELU }_{ \alpha }\begin{cases} x,\quad x\quad >\quad 0 \\ \alpha ({ e }^{ x }\quad -\quad 1),\quad x\quad \le \quad 0 \end{cases}\)
      • 장점 : \(𝑥=0\)일 때, 그레디언트가 급격하게 변하지 않음 (미분은 불가능)
      • 단점 : 계산속도가 상대적으로 느림
  • [ \(ELU > LeakyReLU > ReLU > tanh > sigmoid\)] 순으로 사용하는 것을 권장한다.

배치 정규화

  • 적절한 활성 함수와 초기화 방법을 사용하더라도 내부 공변량 변화에 따라서 그레디언트 소실과 폭주가 발생 할 수 있다.
  • 내부 공변량 변화 : 훈련하는 동안 이전 층의 파라미터가 변함에 따라 각 층에 들어오는 입력의 분포가 변화되는 문제 (학습 데이터과 테스트 데이터가 다른 경우는 공변량 변화라고 한다.)
  • 각 층에서 활성함수를 적용하지 전에 아래 과정을 추가 한다.
    1. 입력 데이터의 평균과 분산을 계산한다. (입력데이터 중 미니배치에서 산출)
    2. 계산된 평균과 분산을 이용하여 평균을 0으로 정규화 한다.
    3. 스케일링과 이동을 담당하는 매개변수를 추가 한다.
      • 위 과정을 수식으로 표현하면 아래와 같다.
      1. \[{ \mu }_{ B } = \frac { 1 }{ { m }_{ B } } \sum _{ i=1 }^{ { m }_{ B } }{ { x }^{ (i) } } ,\quad { \sigma }_{ B }^{ 2 } = \frac { 1 }{ { m }_{ B } } (\sum _{ i=1 }^{ { m }_{ B } }{ { ({ x }^{ (i) }-{ \mu }_{ B }) }^{ 2 } }\]
      2. \[{ \hat { x } }^{ (i) } = \frac { { x }^{ (i) }-{ \mu }_{ B } }{ \sqrt { { \sigma }_{ B }^{ 2 }\quad +\quad \varepsilon } }\]
      3. \[{ Z }^{ (i) } = \gamma { \hat { x } }^{ (i) } + \beta\]
        • \({ \mu }_{ B }\)는 미니배치 \(B\)에 대한 평균 이다.
        • \({ \sigma }_{ B }\)는 미니배치 \(B\)에 대한 표준편차이다.
        • \({ m }_{ B }\)는 미니배치 \(B\)의 샘플 수이다.
        • \({ \hat { x } }^{ (i) }\)는 평균이 0이고 정규화된 입력이다.
        • \(\gamma\)는 층의 스케일 매개변수이다.
        • \(\beta\)는 층의 이동 (bias) 매개변수이다.
        • \(\varepsilon\)는 분모가 0이 되는 것을 막기 위한 smoothing term이다.
        • \({ Z }^{ (i) }\)은 BN 연산의 출력이다.
  • 배치 정규화가 적용되어진 layer 마다 \(\gamma\)(스케일)), \(\beta\)(이동), \(\mu\)(평균), \(\sigma\)(표준편차)가 추가적으로 학습되게 된다.
  • 테스트 과정에서는 훈련 과정에서 구해진 이동 평균(moving average)을 이용하여 정규화 한다.
  • 이동 평균은 지수 감소(expoonential decay)를 사용해 계산된다.
  • 모멘텀(momentum)이라는 하이퍼 파라미터(hyperparameter)를 적용하여 아래와 같이 계산한다.
    • \[\hat { v } \leftarrow \hat { v } \times momentum + v \times (1 - momentum)\]
    • momentum은 0.9와 같이 1에 가깝게 초기화하며, 미니배치가 작을 경우 더 1에 가깝게 조정한다.
  • 배치 정규화의 장단점
    • 장점
      • 매개변수가 안정되어 더 큰 학습률(learning rate)을 사용 할 수 있다.(학습 속도 향상)
      • 미니배치를 어떻게 설정하는가에 따라 모델이 일반화되어 drop out, l2 regularization에 대한 의존도가 떨어진다.
    • 단점
      • 학습 매개변수가 늘어나 모델의 복잡도가 올라감.
      • 학습 시간과 예측 시간이 오래 걸린다.
  • 빠른 예측을 원한다면, 활성 함수와 초기화 방법을 먼저 튜닝하여 모델을 평가할 것을 권장한다.

그레디언트 클리핑

  • 그레디언트 클리핑은 그레디언트 폭주를 막는 가장 쉬운 방법 중 하나로 역전파될 때 그레디언트가 일정 임계치를 넘지 못하게 막는 것이다.
  • 일반적으로 배치 정규화를 선호한다.

학습 속도 향상

  • DNN은 layer 수가 할수록 학습 속도가 느려 지는데, 앞서 설명된 내용을 포함하여 아래와 같은 방법으로 속도를 향상 시킬 수 있다.
    • 좋은 가중치 초기화 전략 적용
    • 좋은 활성 함수 적용
    • 배치 정규화 적용
    • 미리 학습된 신경망의 일부 재사용
    • 고속 최적화 알고리즘(optimizer) 사용
  • 지금부터 gradient descent 외에 더 빠른 최적화 알고리즘에 대해 알아보자.

Gradient descent 업그레이드

  • 모멘텀 최적화(momentum optimizer)
    • gradient descent는 gradient가 작으면 매우 느려 진다.
    • gradient를 속도가 아니라 가속도로 사용한다.
    • 알고리즘
      1. \[m \leftarrow \beta m + \eta { \nabla }_{ \theta }J(\theta )\]
      2. \(\theta \leftarrow \theta - m\)
        • \(\theta\)는 가중치이다.
        • \(m\)은 모멘텀 벡터이다.
        • \(\beta\)는 모멘텀이다.(0~1사시의 하이퍼 파라미터로 0.9을 일반적으로 사용)
        • \(\beta m\)을 통해 일종의 마찰을 표현하고 있다.
        • gradient descent는 \(\theta \leftarrow \theta - \eta { \nabla }_{ \theta }J(\theta )\)로 가중치를 갱신하다는 곳을 상기하자.
    • 스케일이 매우 다른 입력을 받게 되더라도 빠르게 동작하며, local optima를 건너뛰도록 도움을 준다.
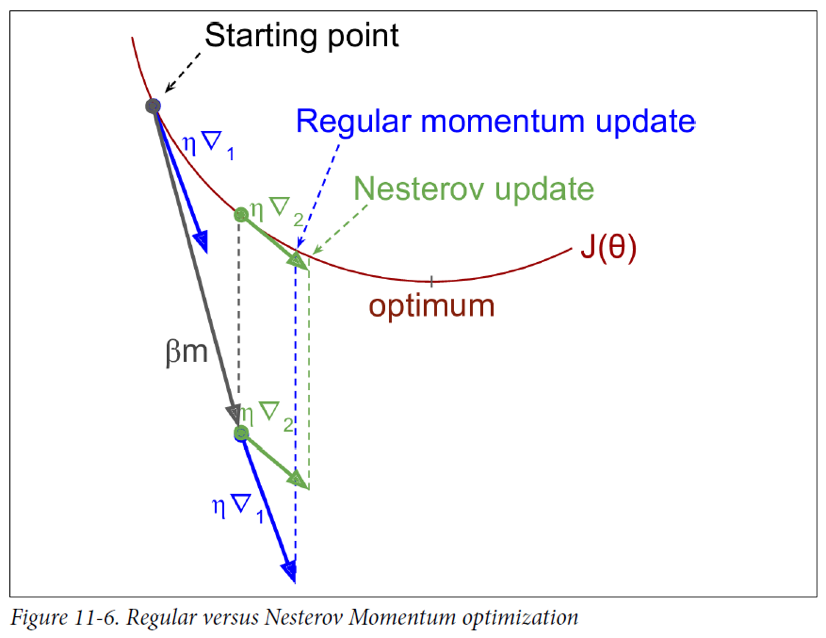
  • 네스테로프 모멘텀 최적화(Nesterov momentum optimizer)
    • 1983년, 유리 네스테로프가 제안했다.
    • \(\theta\)가 \(\theta - \beta m\)의 gradient를 계산하는 것이 기본 모멘텀 최적화와 다른 점이다.
    • 알고리즘
      1. \[m \leftarrow \beta m + \eta { \nabla }_{ \theta }J(\theta - \beta m)\]
      2. \[\theta \leftarrow \theta - m\]
    • 기본 모멘텀 최적화 보다 거의 항상 빠름.
  • AdaGard(Adaptive Subgradient Methods for Online Learning and Stochastic Optimization)
    • 가장 가파른 차원을 따라 그레디언트 벡터의 스케일을 감소시켜 문제를 해결한다.
    • 알고리즘
      1. \[s \leftarrow s + { \nabla }_{ \theta }J(\theta )\otimes { \nabla }_{ \theta }J(\theta )\]
      2. \(\theta \leftarrow \theta - \eta { \nabla }_{ \theta }J(\theta )\oslash \sqrt { s+\varepsilon }\)
        • \(\otimes\)는 원소 별 곱셈을 나타낸다. (element-wise product)
        • \(\oslash\)는 원소 별 나눗셈을 나타내며, \(\)𝜀는 smoothing term이다.
        • 벡터 \(s\)의 원소 \({ s }_{ i }\)마다 \({ s }_{ i } \leftarrow { s }_{ i } + { (\frac { \partial }{ \partial { \theta }_{ i } } J(\theta )) }^{ 2 }\)를 계산한다.
        • 각 매개변수 \({ \theta }_{ i }\)에 대해 \({ \theta }_{ i }\leftarrow { \theta }_{ i }-\eta \frac { \partial }{ \partial { \theta }_{ i } } J(\theta )\div \sqrt { { s }_{ i }+\varepsilon }\)를 계산한 것과 동일하다.
    • 그레디언트가 클수록 \({ s }_{ i }\)도 커지고, \(\sqrt { s+\varepsilon }\)는 작아져서, 가파른 차원에서 학습이 느려 지고 완만한 차원에서 빨리 진행 된다.
    • 학습률이 빠르게 감소하여 전역 최적점에 도달하기 전에 멈출 수 있으므로 DNN에서는 권장하지 않는다. (선형회귀 같은 간단한 작업에는 효과적일 수 있다.)
  • RMSProp
    • AdaGrad가 너무 빠르게 느려 져서 최적점에 도달하기전에 멈추는 문제를 해결하였다.
    • 가장 최근 반복에서 비롯된 그레디언트를 누적하여 해결하였다.
    • 알고리즘
      1. \[s \leftarrow \beta s+(1 - \beta){ \nabla }_{ \theta }J(\theta )\otimes { \nabla }_{ \theta }J(\theta )\]
      2. \(\theta \leftarrow \theta - \eta { \nabla }_{ \theta }J(\theta )\oslash \sqrt { s+\varepsilon }\)
        • \(\beta\)는 감쇠율로 일반적으로 0.9로 설정한다.
    • \(/bata\)라는 하이퍼 파라미터가 추가 되었지만 대부분의 경우 따로 튜닝 할 필요가 없다.
    • 일반적으로 AdaGrad뿐만 아니라 모멘텀 최적화, 네스테로프 최적화보다 성능이 좋다.
  • Adam 최적화(adaptive moment estimation optimizer)
    • 모멘텀 최적화와 RMSProp의 아이디어를 결합하였다.
    • 알고리즘
      1. \[m \leftarrow { \beta }_{ 1 }m + (1-{ \beta }_{ 1 })\eta { \nabla }_{ \theta }J(\theta )\]
      2. \[s \leftarrow { \beta }_{ 2 }s + (1-{ \beta }_{ 2 }){ \nabla }_{ \theta }J(\theta )\otimes { \nabla }_{ \theta }J(\theta )\]
      3. \[\hat { m } \leftarrow \frac { m }{ 1 - { \beta }_{ 1 }^{ T } }\]
      4. \[\hat { s } \leftarrow \frac { s }{ 1-{ \beta }_{ 2 }^{ T } }\]
      5. \(\theta \leftarrow \theta -\eta \hat { m } \oslash \sqrt { s+\varepsilon }\)
        • \(T\)는 반복 횟수이다.
        • 1단계에 우변 2번째 항에 \((1 - { \beta }_{ 1 })\)이 추가 되었다.
        • \(m\)과 \(s\)는 0으로 초기화되기 때문에 0으로 편향되는 것을 막기 위해 3,4번을 적용하여 증폭 시킨다.
    • 모멘텀 감쇠율 \({ \beta }_{ 1 }\)=0.9, 스케일 감쇠율 \({ \beta }_{ 2 }\)=0.999, 학습률 𝜂=0.001을 일반적으로 사용한다. (적응적 학습률 알고리즘이기 때문에 𝜂는 튜닝할 필요가 적다.)
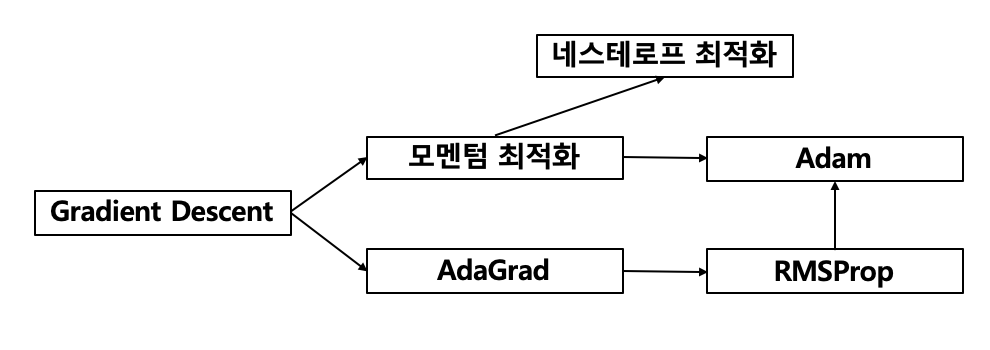
  • optimizer의 변화를 아래와 같이 이해 할 수 있다.

learning rate 스케줄링

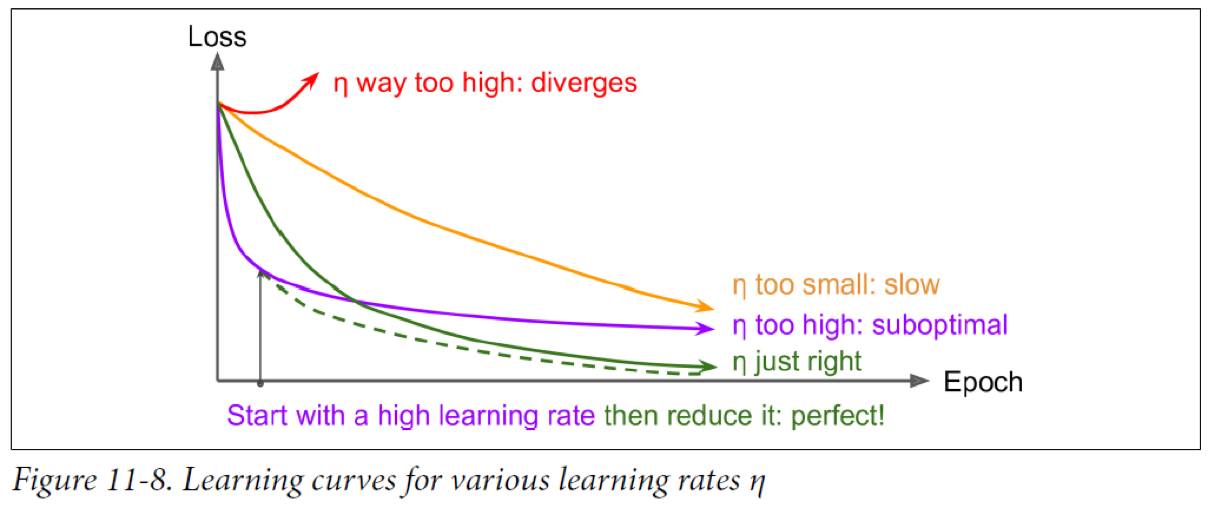
  • 적절한 학습률을 가지는 것이 모델 성능은 물론 학습 속도에서도 중요하다.
  • 학습률이 너무 크면 발산할 수 있으며, 너무 작게 잡으면 최적화 되는데 시간이 매우 오래 걸린다.
  • 리소스가 한정적이라면 차선책으로 완전히 수렴하기 전에 멈추는 방법도 있다.
  • 더 좋은 방법은 학습 중간에 학습률을 변경하는 것이다.
  • 학습률 스케줄링
    • 미리 정의된 고정 학습률
      • 몇 epoch 이후에 학습률을 얼마도 변경 할지 미리 지정해 놓는 방법
      • 적절한 학습률과 적당한 시점을 찾기 위해 튜닝 필요
    • 성능 기반 스케줄링
      • 매 step 마다 검증 오차를 측정하고 오차가 줄어들지 않으면 학습률을 감소시킨다.
    • 지수 기반 스케줄링
      • 매 step \(t\) 의 함수 \(\eta (t) = { \eta }_{ 0 }{ 10 }^{ -t/r }\)을 학습률로 사용한다.
      • 학습률이 매 \(r\)번째 step마다 1/10으로 줄어든다.
      • 하이퍼 파라미터 \({ \eta }_{ 0 }\)과 \(r\)을 튜닝 해야한다.
    • 거듭제곱 기반 스케줄링
      • 매 step \(t\)의 함수 \(\eta (t) = { \eta }_{ 0 }{ 1 + t/r }^{ -c }\)을 학습률로 사용한다.
      • 하이퍼 파라미터 \(c\)는 보통 1로 지정한다.
      • 지수 기반 스케줄링과 비슷하지만 학습률이 더 느리게 감소한다.

Overfitting 방지

  • 아래와 같이 DNN에서 모델을 regularization하여 overfitting을 방지하는 방법을 살펴보자.
    • 조기 종료(early stopping)
    • 드룹아웃(dropout)
    • \({ l }_{ 1 }\)과 \({ l }_{ 2 }\) regularization
    • max-norm regularization

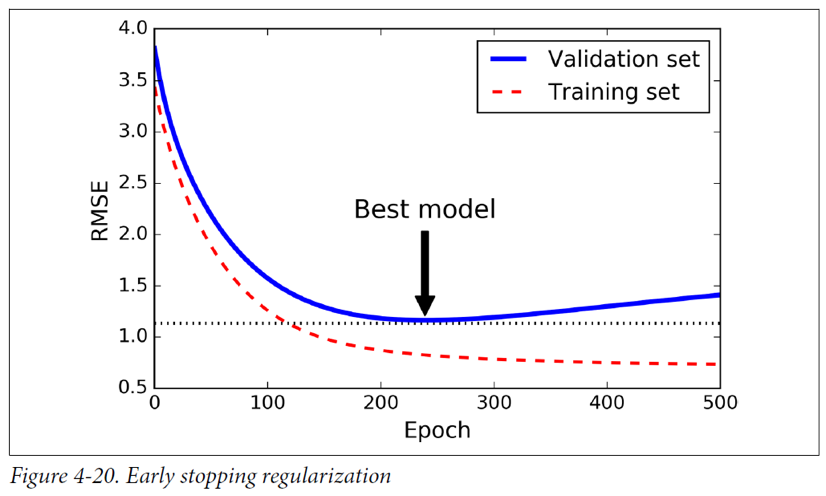
early stopping

  • 학습 과정 중 검증 데이터의 성능이 떨어지기 시작할 때 훈련을 중단하는 것을 의미한다.
  • 매 배치마다 최고 성능의 모델을 스냅샷으로 저장하고, 일정 step 이상 모델이 변화가 없으면 학습을 중단하고 해당 스냅샷을 적용한다.
  • 다른 머신러닝 알고리즘에서도 적용 가능하다.

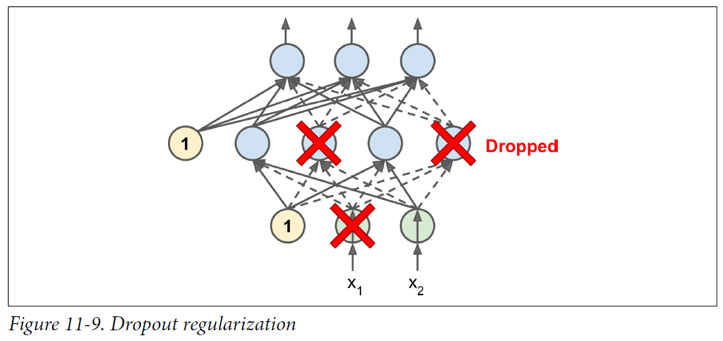
dropout

  • 2012년, 제프리 힌튼에 의해 제안되었다.
  • 매 훈련 스텝에서 각 뉴런이 확률 p에 의해 드롭아웃 된다.
  • 하이퍼 파라미터 p를 dropout rate이라고 한다. (일반적으로 0.5로 초기화)
  • 이렇게 학습하게 되면, 매 step마다 다른 신경망 구조를 가지게 되어 일반화 된다.
  • 매번 각각 다른 신경망을 평균으로 하는 앙상블로 이해할 수 있다.
  • 테스트하는 과정에서 한 뉴런이 평균적으로 두 배 많은 입력 뉴런과 연결되므로 훈련이 끝난 뒤에는 가중치에 보존확률(1-p)를 곱해야 한다.
  • 모델이 과대적합 되었으면 p를 키워야 한다.
  • 모델이 과소적합 되었으면 p를 낮춰야 한다.

\({ l }_{ 1 }\)과 \({ l }_{ 2 }\) regularization

  • 손실 함수(\(L\))에 적절한 규제항을 추가하여 일반화 할 수 있다.
  • \(W = \left[ { w }_{ 1 } { w }_{ 2 } ... { w }_{ n } \right]\)라고 할때,
  • \({ l }_{ 1 }\) regularization
\[{ L }_{ new } := { L }_{ old } + \frac { \lambda }{ 2 } ({ w }_{ 1 }^{ 2 } + { w }_{ 2 }^{ 2 } + { w }_{ n }^{ 2 })\]
  • \({ l }_{ 2 }\) regularization
\[{ L }_{ new } := { L }_{ old } + \lambda (\left| { w }_{ 1 } \right| + \left| { w }_{ 2 } \right| + ... + \left| { w }_{ n } \right| )\]
  • \({ l }_{ 1 } + { l }_{ 2 }\) regularization
\[{ L }_{ new } := { L }_{ old } + \frac { \lambda }{ 2 } ({ w }_{ 1 }^{ 2 } + { w }_{ 2 }^{ 2 } + { w }_{ n }^{ 2 }) + \lambda (\left| { w }_{ 1 } \right| + \left| { w }_{ 2 } \right| + ... + \left| { w }_{ n } \right| )\]

max-norm regularization

  • 가중치 \(W\)의 크기( \({ l }_{ 1 }\) norm )를 특정 임계치보다 작게 제한하는 방법이다.
  • 알고리즘
    • 매 훈련 step에서 \({ \left\| w \right\| }_{ 2 }\) 를 계산한다.
    • \(W\leftarrow W\frac { r }{ { \left\| w \right\| }_{ 2 } }\)으로 가중치를 제한한다.

참고 자료

  • Hands-on machine learning with Scikit-learn & Tensorflow - 오렐리앙 제롱

Related Posts