애자일은 단순히 방법이나 절차로써 정의되는 것이 아니라 가치관 혹은 철학이기 때문에 전체 프로젝트 구성원이 이에 대한 이해 또는 합의가 필수적이다.
그런 관점에서 좀 더 효율적인 데이터 분석 방법론을 설계하기 위해 러셀 저니(Russell Jurney)의 A manifesto for Agile data science을 번역하여 제공한다.
변역 과정 중 일부 의역이 있음을 밝힌다.
또한, **‘애자일 소프트웨어 개발과 애자일 데이터 사이언스는 다르다’라는 저자의 의견을 기억하자.
서론
저는 뭐라고 부르기 전부터 분석 어플리케이션의 반복적이고 진화적인 개발인 애자일 데이터 사이언스를 10년 동안 하고 있습니다.
고독한 풀 스택 개발자로 일하면서 필자가 구축한 분석 소프트웨어를 반복적으로 발전시키는 것은 당연했습니다.
내가 팀에 합류 했을 때, 당연히 그럴 것을 기대했지만 그렇지 않았습니다.
저는 웹 개발자로서 애자일 방법론에 노출되어 있었기 때문에 데이터 사이언티스트로서 일을 시작했을 때 데이터 사이언스가 애자일스럽지(?) 못하다
는 것을 알고 놀랐습니다.
그 직장에 도착한 지 몇 주 안에, 복잡한 예측 시스템을 명시하고 넘겨주어야 했는데 다음 작업자는 배포 전 빌드까지 6개월이나 필요했습니다.
이것은 소프트웨어를 만드는 방법에 대해 알고 있는 모든 것을 위반했지만, 시스템의 규모와 빅데이터 툴의 상태가 이런 상황을 만들었습니다.
그 프로젝트는 거의 실패했고 막판에 회생했습니다. 저는 많은 잠을 포기해야 했고, 몇몇 중요한 교훈을 얻었습니다.
저는 절대 이것을 반복하길 원치 않았습니다. 그래서 여러 성공을 거두며 데이터 사이언스에 애자일을 도입하려고 노력했습니다.
애자일 소프트웨어 개발을 데이터 사이언스에 적용하려고 시작하면서 패턴이 나타나는 것을 보았습니다.
적용의 어려움은 구현의 세부사항에서가 아니라, 소프트웨어 이외에 데이터로 작업할 때 애자일 기회에 대한 사고 방식에 있었습니다.
여러 회사에 걸친 경험을 통해 생각을 정리하면서 저는 애자일 데이터 사이언스 선언문을 개발했습니다.
이 선언문은 해야되는 것보다 생각하는 방법에 초점이 맞춰져있습니다.
Kanban 또는 scrum의 구체적인 내용은 팀이 데이터 탐색으로 부터 도출된 기회에 반응하며 다이나믹하게 생각하기 때문에 데이터 사이언스에 효과가
있다.
John Akred은 애자일 데이터 사이언스의 구현에 흥미로운 연구를 수행해 왔지만, 어떻게 작업을 추적하는지에 대해서는 전혀 알려지지 않았습니다.
핵심은 당신이 적극적이고 역동적인 방식으로 데이터 과학에 접근하는 것입니다.
애자일 데이터 사이언스 선언문
반복하고 반복하고 반복하라.
통찰력은 한번에 나오는 것이 아니라 25번의 연속적인 쿼리로부터 나온다.
데이터 테이블들을 파싱하고, 형식화하고, 정렬하고, 집계하고, 요약해야 한다.
의미있는 도표는 일반적으로 첫번째 시도가 아니라 3번에서 4번은 거쳐야 얻어진다.
정확한 예측 모델을 설계하는 것은 많은 특성 공학(feature engineering)과 하이퍼파라미터 튜닝(hyperparameter tuning)으로 부터 얻어 질수 있다.
데이터 사이언스에서 반복은 추출, 시각화, 통찰력의 제품화를 하는데 본질적인 요소이다. 우리는 설계할 때, 우리는 반복한다.

중간 결과를 공유하라.
반복은 분석 어플리케이션 제작에서 필수적인 행동이며, 이는 종종 스프린트 끝에 완전 하지 않을 것을 남기게 한다.
우리가 스프린트 끝에 완전하지 않은 혹은 중간 결과를 전달하지 않는다면 아무것도 전달하지 못할 것이다. 그리고 이것은 애자일이 아니다.
나는 이와 같이 누구도 원하지 않는 완벽한 것에 끊임없이 시간을 낭비되는 것을 죽음의 고리(death loop)라고 부른다.
좋은 시스템은 스스로 문서화 한다. 애자일 데이터 사이언스에서 우리는 우리가 작업한 불완전한 자신을 문서화하고 공유한다.
소스 컨트롤러에 모든 작업을 커밋한다. 우리는 이 작업을 팀원가 공유하고, 가능하다면 최종 사용자도 같이 한다.
이 원칙이 모두에게 설득력 있게 다가오지 않을 것이다.
많은 데이터 사이언티스트는 다년간의 격렬한 연구 끝에 얻어낸 학위 논문을 배경으로 하는 자신만의 지론을 갖고 있기 때문이다.

작업이 아니라 실험을 하라.
소프트웨어 공학에서 제품 관리자는 스프린트 중에 개발자에게 표를 넘겨줄 것이다.
개발자는 넘겨받은 표를 SQL GROUP BY로 데이터베이스에 저장하고, 그것을 표시할 웹페이지를 만든다. 이걸로 할 일이 끝난 것인가? 아니다.
그런 식으로 저장된 표는 가치있는 것 같지 않다. 데이터 사이언스는 과학 부분과 공학 부분이 있다는 점에서 소프트웨어 공학과 다르다.
맞닥뜨린 모든 과제에서 우리는 통찰력을 얻기 위해 반복해야 하며 이런 반복은 실험으로써 가장 잘 요약될 수 있다.
데이터 사이언스 팀을 관리 한다는 것은 작업을 나눠주는 것보다 여러 가지 동시 실험을 감독하는 것을 의미한다.
좋은 자산(테이블, 표, 보고, 예측)은 탐색적 데이터 분석의 결과물로 나타나므로 작업보다 실험 측면에서 더 많이 고려해야 한다.
데이터에 귀를 기울어라.
‘무엇이 가능한가’는 ‘무엇을 의도 했는가’만큼 중요하다.
‘무엇이 쉽고 무엇이 어려운것’은 ‘무엇을 원하는가’를 아는 것 만큼 중요하다.
소프트웨어 어플리케이션 개발에서 고객, 개발자, 비지니스 세가지 관점을 고려 해야한다.
분석 어플리케이션 개발에서 또하나의 관점은 데이터이다.
모든 기능에 대해 데이터가 ‘무엇을 말하고 이는지’를 이해하지 못하면 제품 소유자는 훌륭한 일을 할 수 없다.
제품 회의에는 항상 데이터에 관한 의견이 포함되어 있어야 한다.
즉, 제품은 우리가 많은 노력을 쏟는 탐색적 데이터 분석을 통한 시각화에 기반을 두고 있어야 한다는 것을 의미한다.
데이터 가치 피라미드를 따라라.
데이터 가치 피라미드는 Maslow의 수요 체계도에 따라 5개의 계층으로 구성되어 있다.
이 피라미드는 원본 데이터가 표, 차트, 보고, 예측을 이어지면서 데이터의 가치가 증가 하는 것을 표현한다.
이 일련의 과정은 새로운 행동을 가능하게 하거나 기존 데이터를 개선하기 위한 것이다.
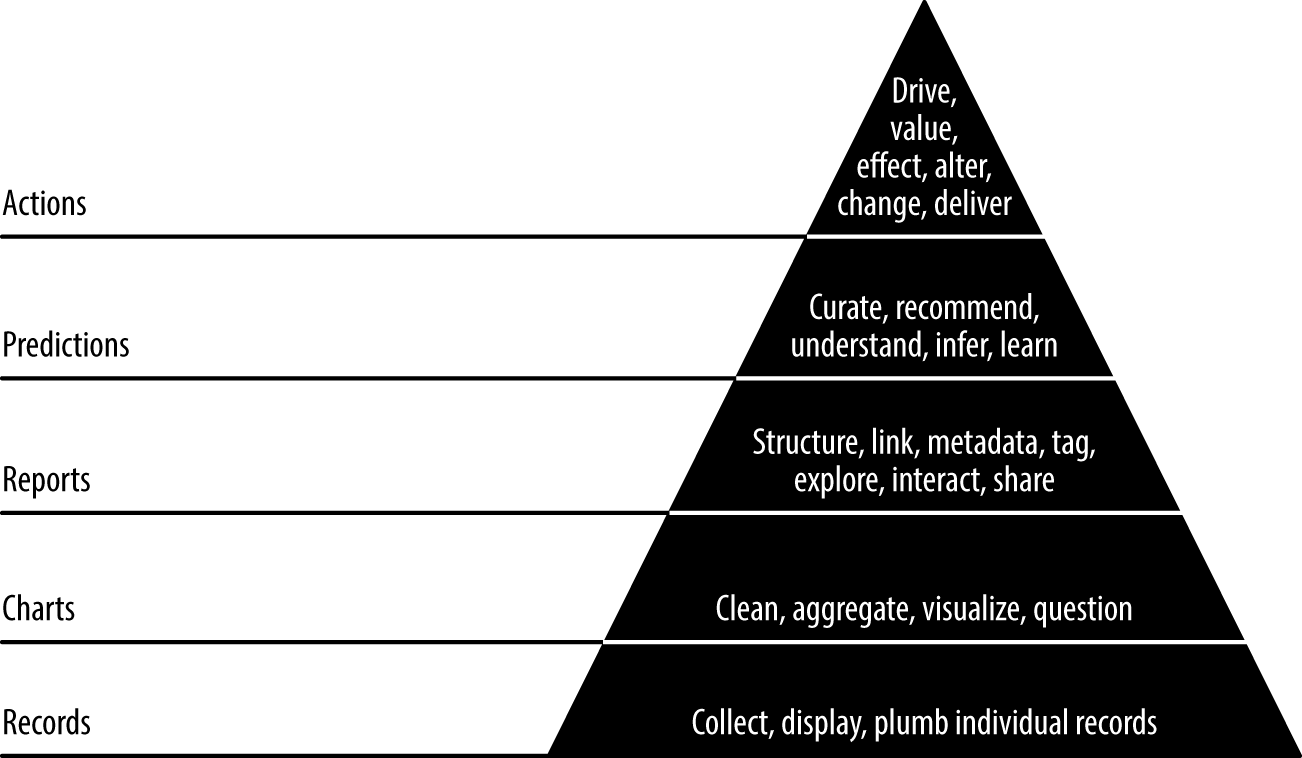
- Records : 데이터가 수집된 위치에서 어플리케이션에 나타낼 수 있는 위치로 데이터를 흐르게 하는 과정이다.
- Charts : 정제와 분석이 시작되는 단계이다.
- Reports : 데이터에 대한 몰입적 탐구를 가능하게 할 수 있다. 여기에서 실제로 데이터를 추론하고 이해 할 수 있다.
- Predictions : 더 많은 가치가 창출되는 곳이다. 피쳐 엔지니어링(feature engineering)을 통해 더 좋은 예측을 만들어 낼 수 있다.
- Actions : 인공지능 열풍이 일어나는 단계이다. 귀하의 통찰력이 새로운 행동을 가능하게 하지거나 기존의 행동을 개선 시키지 않는다면 그다지 중요하지 않다.
데이터 가치 피라미드는 우리의 작업을 구조화 한다.
이 피라미드는 꼭 따라야 할 규칙은 아니지만, 명심하고 있어야 한다.
어떤 때는 단계를 건너뛰기도 하고, 또 어떤 때는 이전 단계로 돌아가야 할 것이다.
만약 당신이 어떤 데이터를 곧바로 예측 모델에 집어넣어 버린다면, 낮은 계층에서 데이터를 투명하고 접근할 수 있게 만들어두지 않는다면, 기술적인 문
제가 발생 할 것이다.
이런 점을 명심하고, 가능하다면 생길 수 있는 문제를 미리 예방하자.
핵심 경로를 찾아라.
성공 확률을 극대화하려면 대부분의 시간을 성공의 핵심 요소인 어플리케이션 측면에 집중해야 한다.
하지만 그런 부분은 어디일까? 그것은 실험을 통해 발견됨에 틀림없다.
분석 제품 개발은 움직이는 목표를 찾고 추구 하는 것이다.
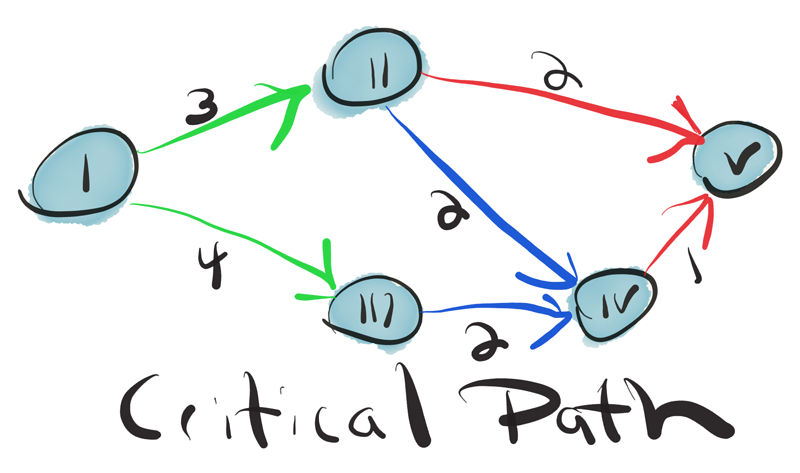
예를 들어, ‘어떤 예측을 해야한다.’하는 목표가 정해졌다면, 우선 구현하는 데 있어 중요 경로를 찾아 내야하며 가치가 있다고 판단되면 개선해야 한다.
데이터는 작업이 진행됨에 따라 점진적으로 정제된다.
분석 제품은 종종 광범위한 ETL(추출, 변화, 로드), 프로세스, 통계, 정보 접근, 머신러닝, 인공 지능 및 그래픽 분석의 기술을 사용한다.
이런 단계의 상호 작용은 종속적인 복잡한 웹을 형성할 수 있다.
팀 리더는 이러한 의존 요소를 항상 기억하고 있어야 한다.
팀원이 중요한 경로를 발견해 그 경로를 따라갈 수 있도록 이끄는 것도 리더가 해야할 일이다.
제품 관리자는 top-down 형식으로 이런 과정을 이끄는 것은 불가능한 일이다.
그보다는 제품 과학자가 bottom-up 형식으로 발견해야 한다.
메타를 얻어라.
만약에 일반적인 어플리케이션을 개발할 때랑 비슷한 일정으로 좋은 제품을 전달하기가 쉽지 않다면 어떻게 하면 좋을까?
전달하지 않는다면 그것은 애자일이라고 부를 수 없다.
애자일 데이터 사이언스에서 이 문제를 해결하기 위해 “메타를 얻는다”.
추구하는 최종 상태 또는 제품과 반대로 분석 프로세스를 문서화 하는데 초점을 둔다.
이렇게 하면 데이터 가치 피라미드를 반복적으로 올라가 killer product의 중요 경로를 찾을 때 민첩하게 되고 중간 결과를 전달 할 수 있다.
이런 제품은 어떻게 얻을 수 있을까? 우리는 탐색적 데이터 분석을 문서화하면서 만든다.

결론
이 7가지 원리는 애자일 데이터 사이언스 방법론을 가능하게 해준다.
이것들은 탐색적 데이터 분석 프로세스를 구조화 및 문서화하여 분석 어플리케이션으로 변화하는 역할을 한다.